机器学习
机器学习
机器学习学习小总结
本文档使用 WYMF 发布
-
+
首页
机器学习学习小总结
# 机器学习学习小总结 ## 机器学习的主要分类 监督学习和无监督学习 ### 监督学习主要还分为 1.回归 2.分类 1.回归 ------ 可以理解为数字预测,给定一个输入 x,通过某个模型输出一个确定的值 y。  2.分类 ------ 与回归大致相同,只不过通过模型输出的是一个类别,类别的个数是有限的,输出类别的其中之一。 - 注意,以上通过模型输出的均是预测值。 ### 无监督学习 其中最常见的是类聚算法,举个例子 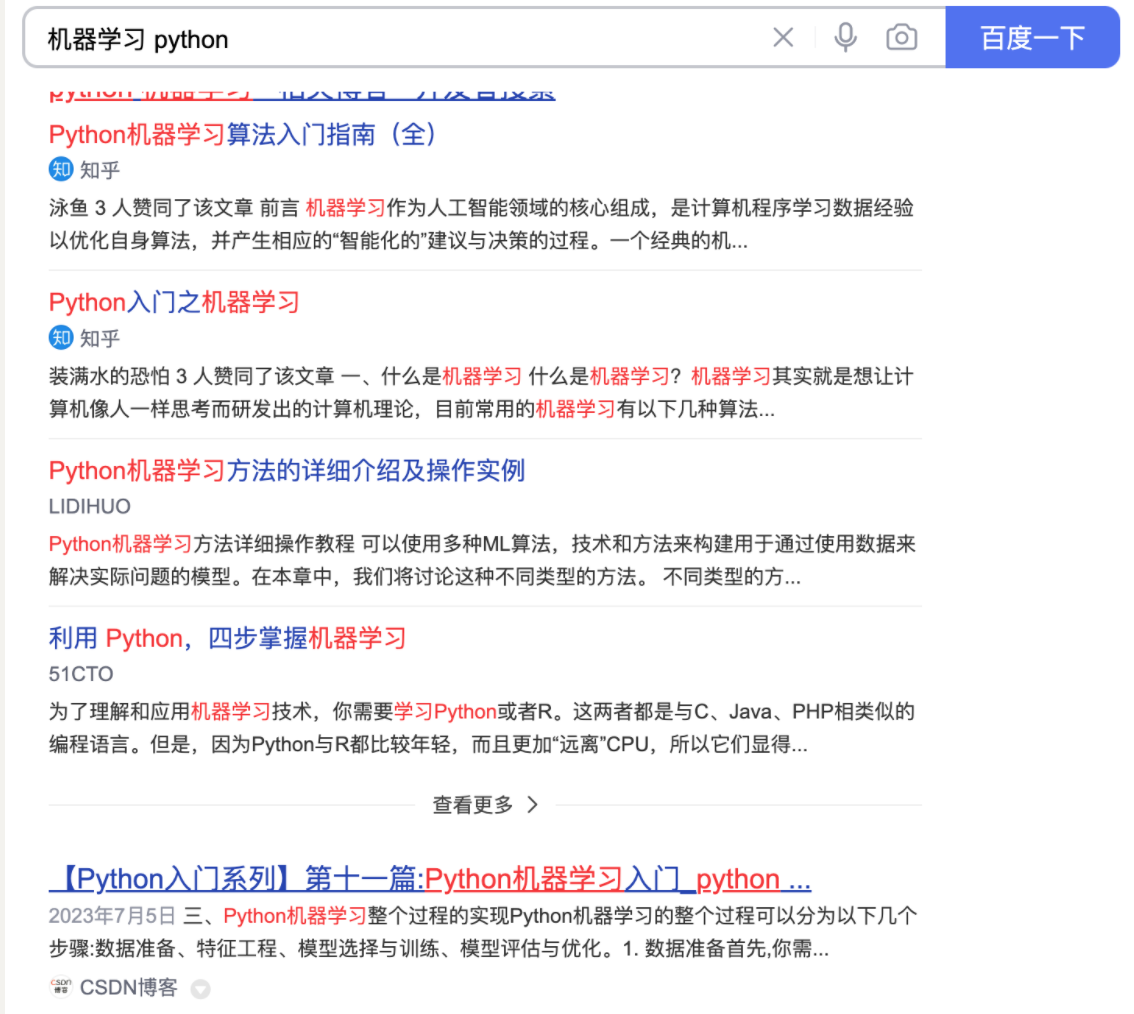 例如,我们打开百度,输入 机器学习 python,就会给我们呈现这些我们可能需要的,每一项都有 <span style="color:red;"> 机器学习 python </span> 这两个关键字,所以聚类算法就可以理解为,你要去百度 找你想要的 东西。 ### 网上有成千上万条,我们要找的东西,都是通过 <span style="color:red;"> 聚类算法和关键字 </span>,将它们进行分类。 ## 几个比较重要的概念 ### 损失函数,成本函数 这个成本函数就是间接的看出预测值与真实值的差距,成本函数越大预测的越不准,(可以理解为成本大),成本函数越小预测的越准确。 损失函数与成本函数都是计算,真实值与预测值的差,只不过区别在于 <span style="color:red;"> 损失函数 </span> 是单个样本,而 <span style="color:red;"> 成本函数 </span> 是对 m 个样本计算误差 - 常见的损失函数有,平方差损失函数,交叉熵损失函数 多用于回归 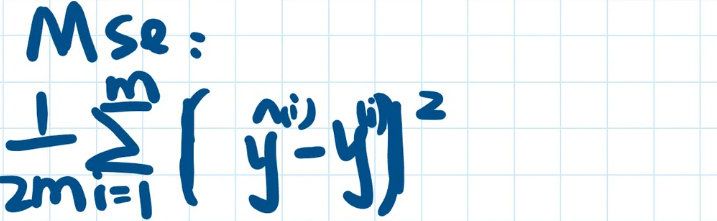 多用于二分类 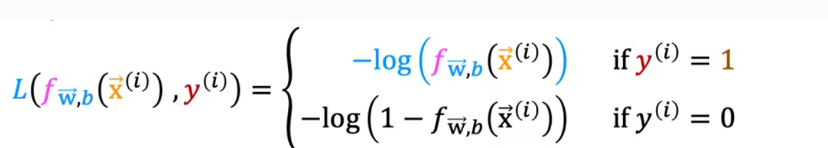 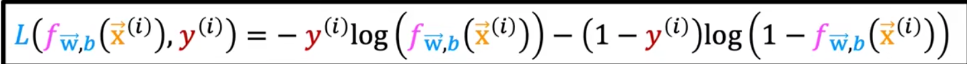 ### 模型 - 常见的模型 线性回归模型,逻辑回归模型,神经网络。 线性回归模型: f$_{w,b}$(x)=$\vec{w}$$\cdot$$\vec{x}$+b 逻辑回归模型: - 首先我们需要一个像 ==线性回归模型==的直线函数 f$_{w,b}$(x)=$\vec{w}$$\cdot$$\vec{x}$+b 我们将($\vec{w}$$\cdot$$\vec{x}$+b) 存在 z 这个变量里 即 z=$\vec{w}$$\cdot$$\vec{x}$+b - 再将 z 传入到 Sigmoid 函数中即 g(z)=$\frac{1}{1+e^{-z}}$,然后根据 Sigmoid 函数输出对应的值,如下图所示。 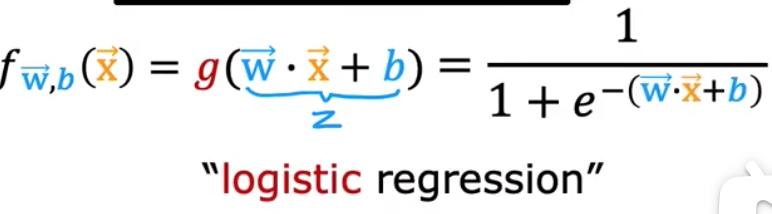 ### 多层感知机模型: 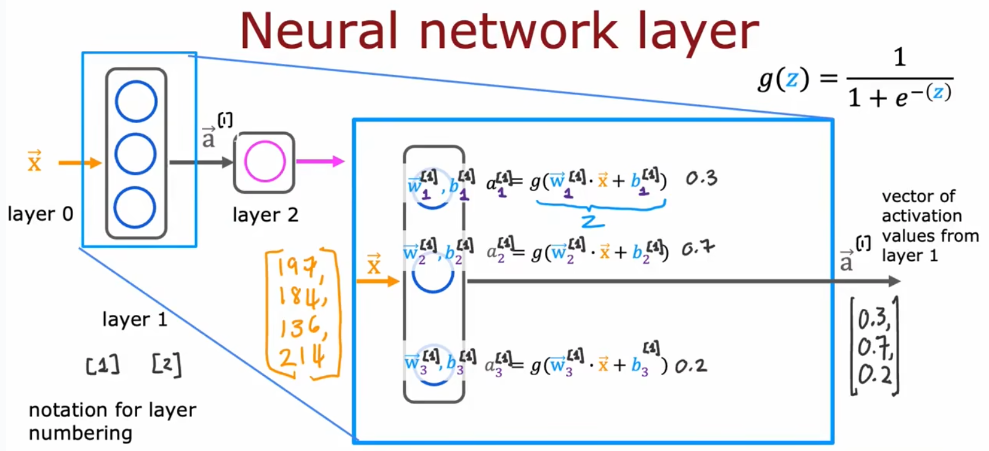 如图, $\vec{x}$ 为 layer0,有三个 蓝色 神经元的一层为第一隐藏层,他的工作原理,如图所示,每一个神经元中都有参数,每一个神经元也会输出一个值,将这三个神经元共同输出的值,也叫 =激活值= ,重新组成一个向量 **a**,作为下一层的输入。 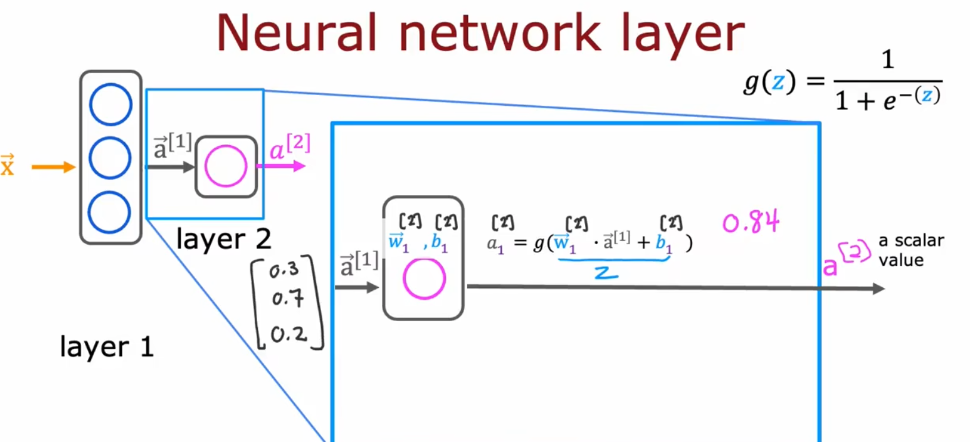 第二层神经元的工作原理与第一层相似。因为第二层==只有一个神经元== ,即最后输出的不是一个 $\vec{a}$,而是一个数字。 卷积神经网络模型: ### 梯度下降与成本函数 ==梯度下降的目的==,为模型找到合适的参数,这里我们拿==线性模型== 举例子, 设想一下你有一些数据,你要用一条直线去拟合他们,如下图 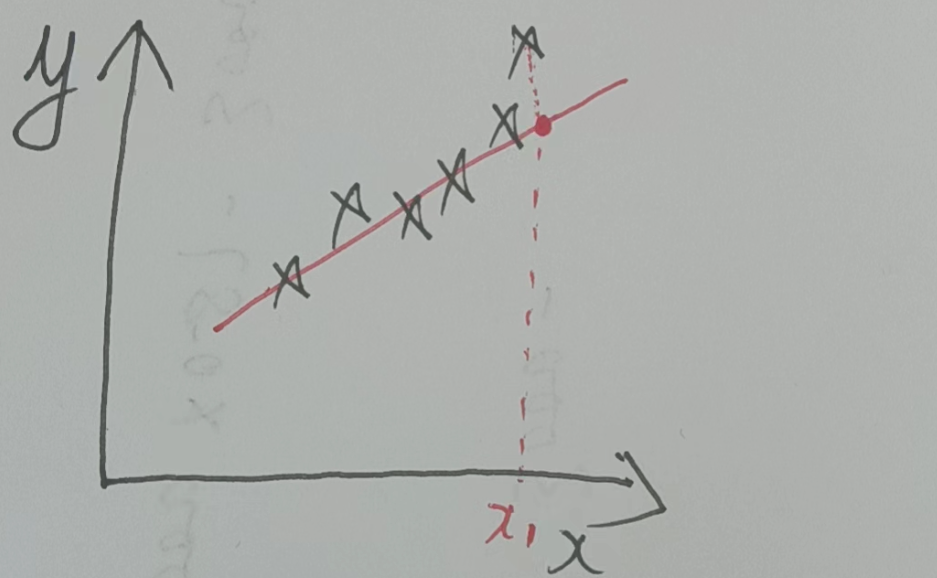 红色直线为拟合直线(直线上的值都是预测值),当 x=x~1~ 时,可见预测值与真实值有一段距离,这段距离我们称为==误差== 。 这条直线 $\widehat{y}$=f<sub>w,b</sub>(x<sup>(i)</sup>)=wx<sup>(i)</sup>+b 我们拿平方误差函数作为==成本函数==(cost function)。分为以下几个步骤。 1.算出预测值与真实值的差,$\widehat{y}$-y 2.将其平方,($\widehat{y}$-y)<sup>2</sup> 3.将整个训练集的 真实值与预测值差的平方加和 $\sum_{i=1}^m$ ($\widehat{y}$-y)平方 4.注意,随着训练量的增加你的 cost function 会变大,所以我们要除以训练集个数 m, 5.但是按照惯例,我们处于 2m,方便后面的计算 即 J(w,b)= $\frac{1}{2m}$ $\stackrel{m}{\sum\limits_{i=1}} f_{w,b}(x^{(i)}-y^{(i)})^2$ 不同的 model 用不同的 J,平方误差成本函数是迄今最适合用于线性回归的,J(w,b)也可以写成 J(w,b)= $\frac{1}{2m}$ $\stackrel{m}{\sum\limits_{i=1}} f_{w,b}(x^{(i)}-y^{(i)})^2$ 最终,我们将要找到使成本函数变小的 w,b。 ### 五 梯度下降 上面我们讲了==成本函数==J,接下来我们要利用==梯度下降算法==去寻找 w 和 b。 你现在有 J(w,b),你想要将其最小化,理论上梯度下降是一种算法,它可以最小化任何成本函数函数,不仅仅是线性回归的成本函数。 首先,我们对 w,b 有一个初步的假设,在线性回归中,w,b 的值是多少不重要,一般我们将他们==设置为 0==。 而你要做的事没次更改 w,b 来尝试降低 J,知道 J 达到或接近最小值。 截屏 2023-11-11 下午 9.10.54 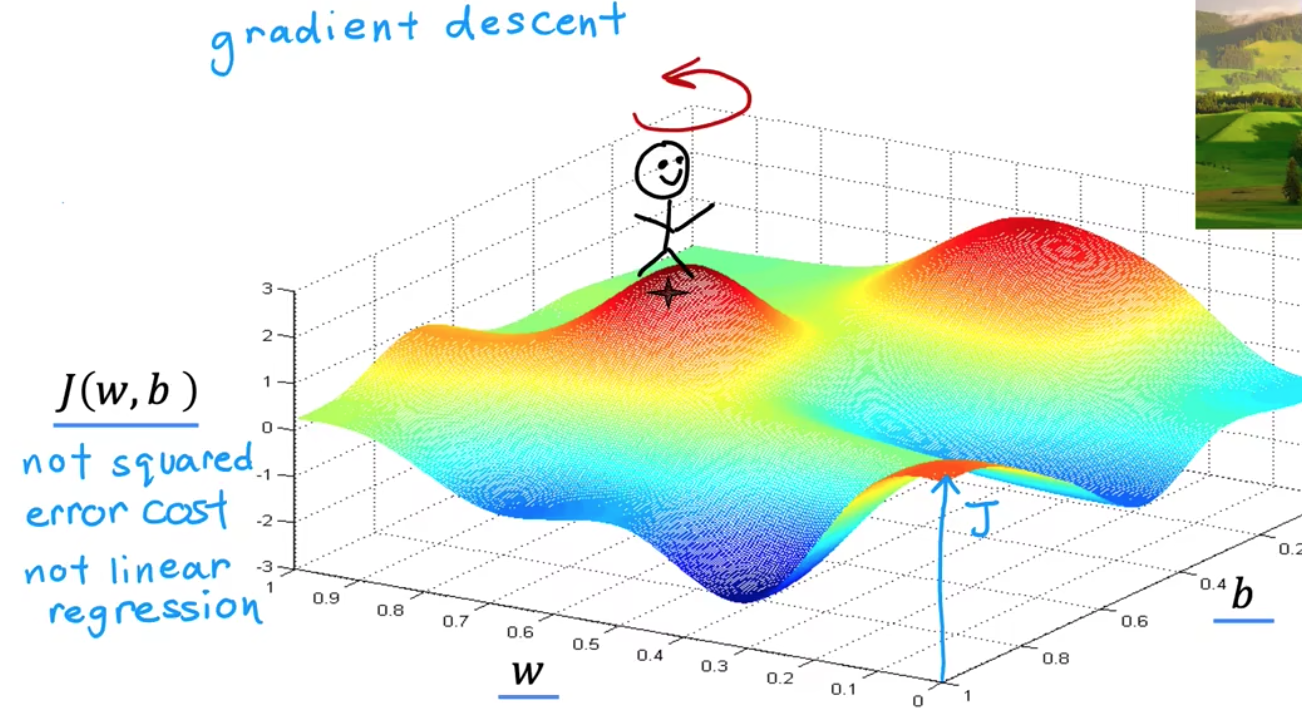 - 对于上图,它存在着多个局部最小值,因此该图不是平方误差损失函数的 J,即也不是线形回归,这是一种训练神经网络可能会用到的成本函数 <span style="color:red;"> 重要的来了: </span> 对于上图,不同的 w 和 b,决定了不同的 J,不同的 J 也代表你在山的不同的高度,==梯度下降所做的是==,你环顾四周,问问自己,你要下山或者到达这些==山谷之一==,你要朝着哪一方向迈出==一小步==(不断的重复),下山最快。 以此类推,知道发现自己已经处在谷底(局部最小值)。 解释一波局部最小, 注意: 为何叫局部最小,是因为最开始选的 w 和 b 不同,导致起点不同,如下图,我们起点选的不同会导致我们到达两个不同的谷底。 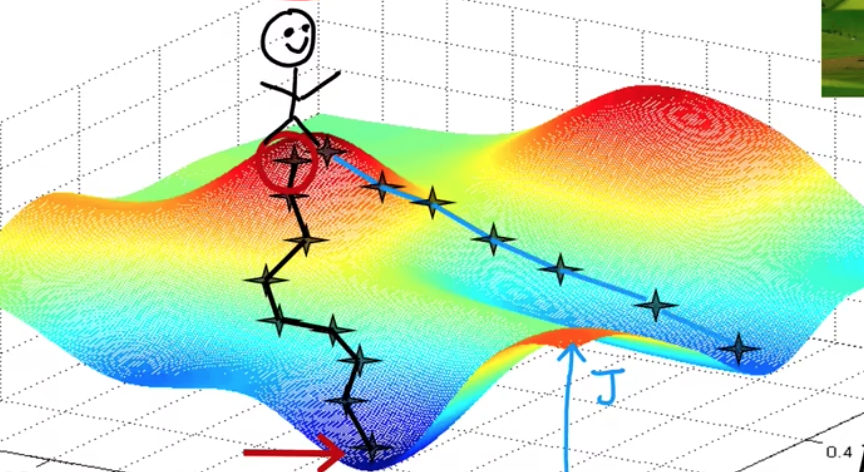 因此,你的起点不同,==梯度下降==会把你带到不同的谷底,你如上图,你在左边的位置,==梯度下降==不会把你带到第二个谷底,这是梯度下降的特性。 ### 5.2 梯度下降的实现 如何实现梯度下降,答案是==我们不断调整 w,b==,如下图 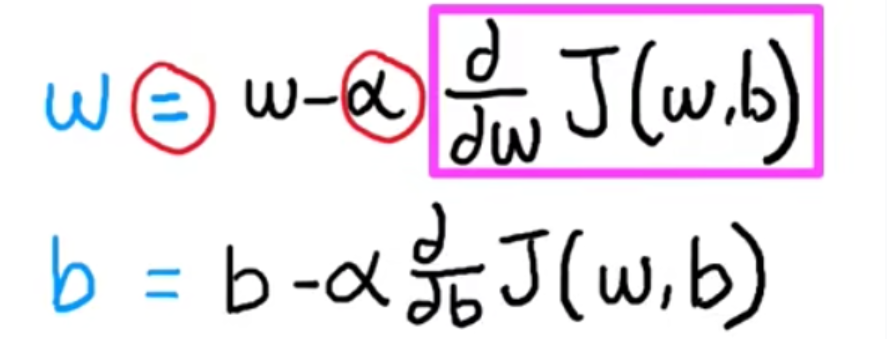 其中 alpha 为学习率,值为[0,1]之间,怎么选择不过多介绍。 梯度下降所做的是,重复 w 和 b 的操作,直至达到一个局部最小值的点。 一个小细节,要同时去更新 w 和 b 这两个参数
我有魔法
2024年3月9日 19:35
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码